Algorithms of artificial intelligence and machine learning are of increasing importance for control applications. Our research and expertise in this domain ranges from the modeling of unknown or uncertain dynamics over iterative and reinforcement learning to Bayesian optimization.
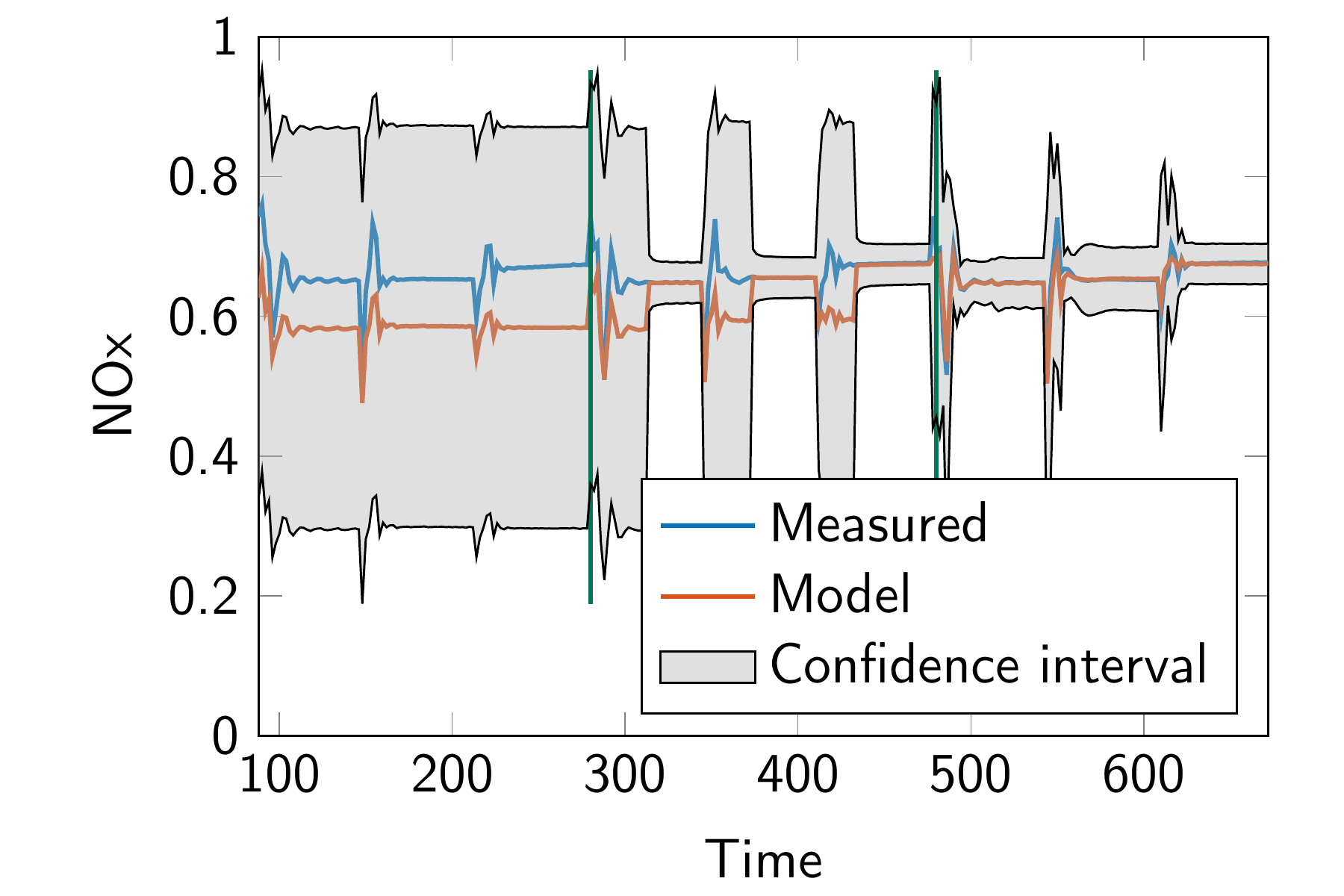
One research focus at the Chair is on learning in model design and identification. Hybrid and data-driven models are attractive if physical modeling is either poor or requires high effort. Practical applications often require an online adaptation of these models in order to reflect effects of aging or wear or to increase the model accuracy in different operation regimes. Information about the reliability and trustworthiness of a learned model can directly be used within the control design. For instance, the prediction of the uncertainty allows to satisfy constraints with a given probability. A challenge with learning-based methods is to ensure real-time feasibility with possibly weak hardware resources in order to bring these advanced learning in control methods into practice.
Another field of research and expertise is learning in optimization and control, for instance, reinforcement learning and Bayesian optimization. Reinforcement learning aims at obtaining an optimal control strategy from repeated interactions with the system. Formulating this task as an optimization problem shows the conceptual similarity to model predictive control, with the difference that reinforcement learning does not require model knowledge of the system. In a similar spirit, Bayesian optimization allows to solve complex optimization problem, in particular if the cost function or constraints are not analytically known or can only be evaluated by costly numerical simulations. Many technical tasks such as the optimization of production processes, an optimal product design or the search of optimal controller setpoints can be formulated as (partially) unknown optimization problem, illustrating the generality and importance of Bayesian optimization.
Related projects since 2023
Term: 1. August 2023 - 31. July 2024
Funding source: Industrie
Project leader:
Funding source: Industrie
Project leader:
Prof. Dr.-Ing. Knut Graichen
Chair holder
Term: 1. February 2024 - 31. January 2026
Funding source: Bundesministerium für Wirtschaft und Energie (BMWE)
Project leader:
Funding source: Bundesministerium für Wirtschaft und Energie (BMWE)
Project leader:
Prof. Dr.-Ing. Knut Graichen
Chair holder
Term: 1. July 2024 - 30. June 2027
Funding source: Industrie
Project leader:
Funding source: Industrie
Project leader:
Prof. Dr.-Ing. Knut Graichen
Chair holder
Term: 1. November 2024 - 30. April 2026
Funding source: Industrie
Project leader:
Funding source: Industrie
Project leader:
Prof. Dr.-Ing. Knut Graichen
Chair holder
Term: 1. September 2024 - 31. August 2025
Funding source: Industrie
Project leader:
Funding source: Industrie
Project leader:
Prof. Dr.-Ing. Knut Graichen
Chair holder
Related publications
- , , , :
Toward Fully Autonomous Driving: AI, Challenges, Opportunities, and Needs
In: IEEE Access (2026)
ISSN: 2169-3536
DOI: 10.1109/ACCESS.2026.3659192
URL: https://ieeexplore.ieee.org/document/11367669
- , , , , :
Aerodynamic neural network modeling for gradient-based model predictive flight control
33rd Mediterranean Conference on Control and Automation (MED 2025)
In: Proc. 33rd Mediterranean Conference on Control and Automation (MED 2025) 2025 - , , , :
Fault Handling in Robotic Manipulation Tasks for Model Predictive Interaction Control
In: IEEE Robotics and Automation Letters 10 (2025), p. 9002-9009
ISSN: 2377-3766
DOI: 10.1109/LRA.2025.3592069 - , :
Learning-based uncertainty-aware predictive control of truck-trailer systems in rough terrain
19th IEEE International Conference on Control & Automation (ICCA) (Tallinn (Estonia), 30. June 2025 - 3. July 2025) - , , , , :
Estimation of input rotation speed in gauge-sensorized strain wave gears
2025 IEEE Conference on Control Technology and Applications (CCTA) (San Diego (USA), 25. August 2025 - 27. August 2025)
DOI: 10.1109/CCTA53793.2025.11151315 - , , , , :
Model-based fault simulation and detection for gauge-sensorized strain wave gears
11th Vienna International Conference on Mathematical Modelling (MATHMOD 25) (Vienna (Austria), 19. February 2025 - 21. February 2025)
In: IFAC PapersOnline 2025
DOI: 10.1016/j.ifacol.2025.03.047 - , , :
A software framework for stochastic model predictive control of nonlinear continuous-time systems (GRAMPC-S)
In: Optimization and Engineering (2025)
ISSN: 1389-4420
DOI: 10.1007/s11081-025-10006-z - , , :
Stochastic model predictive control with switched latent force models
In: European Journal of Control 85 (2025), p. 101311
ISSN: 0947-3580
DOI: 10.1016/j.ejcon.2025.101366 - , , :
A Model Predictive Control Approach to Trajectory Tracking with Human-Robot Collision Avoidance
2025 IEEE Conference on Control Technology and Applications (CCTA) (San Diego, 25. August 2025 - 27. August 2025)
In: Proceedings 9th IEEE Conference on Control Technology and Applications (CCTA) 2025 - , , :
Generalized tolerance optimization for robust system design by adaptive learning of Gaussian processes
In: IEEE Access 13 (2025), p. 68959-68983
ISSN: 2169-3536 - , , , :
Why engineers should care about semi-infinite programming: Nominal versus tolerance-aware geometry optimization of a proportional electromagnetic actuator
10th IFAC Symposium on Mechatronic Systems & 14th Symposium on Robotics (MSROB 2025) (Paris (France), 15. July 2025 - 18. July 2025)
In: Proceedings 10th IFAC Symposium on Mechatronic Systems & 14th Symposium on Robotics (MSROB 2025) 2025 - , , , :
AI safety assurance for automated vehicles: A survey on research, standardization, regulation
In: IEEE Transactions on Intelligent Vehicles 10 (2025), p. 4784-4803
ISSN: 2379-8858
DOI: 10.1109/TIV.2024.3496797 - , , , :
Expanding the Classical V-Model for the Development of Complex Systems Incorporating AI
In: IEEE Transactions on Intelligent Vehicles 10 (2025), p. 1790-1804
ISSN: 2379-8858
DOI: 10.1109/TIV.2024.3434515 - , , , , :
A Concept for Efficient Scalability of Automated Driving Allowing for Technical, Legal, Cultural, and Ethical Differences
2025 IEEE 28th International Conference on Intelligent Transportation Systems (ITSC) (Gold Coast (Australia), 18. November 2025 - 21. November 2025) - , , :
Enhancing system self-awareness and trust of AI: A case study in trajectory prediction and planning
36th IEEE Intelligent Vehicles Symposium (IEEE IV 2025) (Cluj-Napoca (Romania), 22. June 2025 - 25. June 2025) - , , , , , :
A New Perspective On AI Safety Through Control Theory Methodologies
In: IEEE Open Journal of Intelligent Transportation Systems 6 (2025), p. 938-966
ISSN: 2687-7813
DOI: 10.1109/OJITS.2025.3585274 - , :
Physics-informed sparse Gaussian processes for model predictive control in building energy systems
11th Vienna International Conference on Mathematical Modelling (MATHMOD 25) (Vienna (Austria), 19. February 2025 - 21. February 2025)
In: IFAC-PapersOnLine 2025
DOI: 10.1016/j.ifacol.2025.03.009
URL: https://www.sciencedirect.com/science/article/pii/S2405896325002265 - , , :
Application of stochastic model predictive control for building energy systems using latent force models
In: At-Automatisierungstechnik 73 (2025), p. 441-450
ISSN: 0178-2312
DOI: 10.1515/auto-2024-0160
URL: https://www.degruyterbrill.com/document/doi/10.1515/auto-2024-0160/html
- , :
A sensitivity-based approach to self-triggered nonlinear model predictive control
In: IEEE Access 12 (2024), p. 153243-153252
ISSN: 2169-3536
DOI: 10.1109/ACCESS.2024.3480522 - , , , :
DMP-based path planning for model predictive interaction control
European Control Conference (Stockholm (Sweden), 25. June 2024 - 28. June 2024) - , , :
A Programming by Demonstration Approach for Robotic Manipulation with Model Predictive Interaction Control
2024 IEEE Conference on Control Technology and Applications (CCTA) (Newcastle upon Tyne, United Kingdom, 21. August 2024 - 23. August 2024) - , , , , :
Fault detection in gauge-sensorized strain wave gears
European Control Conference (Stockholm (Sweden), 25. June 2024 - 28. June 2024)
DOI: 10.23919/ECC64448.2024.10591216 - , , :
Sampling for model predictive trajectory planning in autonomous driving using normalizing flows
35th IEEE Intelligent Vehicles Symposium (IEEE IV 2024) (Jeju Island (Korea), 2. June 2024 - 5. June 2024)
In: Proc. 35th IEEE Intelligent Vehicles Symposium (IEEE IV 2024) 2024 - , :
PINN-based dynamical modeling and state estimation in power inverters
2024 IEEE Conference on Control Technology and Applications (CCTA) (Newcastle upon Tyne, UK, 21. August 2024 - 23. August 2024) - , , , , :
Sensitivity-based moving horizon estimation of road friction
European Control Conference (Stockholm (Sweden), 25. June 2024 - 28. June 2024) - , , :
Transfer learning study of motion transformer based trajectory predictions
35th IEEE Intelligent Vehicles Symposium (IEEE IV 2024) (Jeju Island (Korea), 2. June 2024 - 5. June 2024)
In: Proc. 35th IEEE Intelligent Vehicles Symposium (IEEE IV 2024) 2024 - , , :
Occupancy Prediction for Building Energy Systems with Latent Force Models
In: Energy and Buildings (2024), p. 113968
ISSN: 0378-7788
DOI: 10.1016/j.enbuild.2024.113968
- , , , :
Safe active learning and probabilistic design of experiment for autonomous hydraulic excavators
2023 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) (Detroit, 1. October 2023 - 5. October 2023) - , , , , , , :
Concept for an Automatic Annotation of Automotive Radar Data Using AI-segmented Aerial Camera Images
2023 IEEE International Radar Conference, RADAR 2023 (Sydney, NSW, 6. November 2023 - 10. November 2023)
In: Proceedings of the IEEE Radar Conference 2023
DOI: 10.1109/RADAR54928.2023.10371183 - , , , , :
Simulation chain for sensorized strain wave gears
27th International Conference on System Theory, Control and Computing (ICSTCC) (Timisoara (Romania), 11. October 2023 - 13. October 2023)
In: Proc. 27th International Conference on System Theory, Control and Computing (ICSTCC) 2023
DOI: 10.1109/ICSTCC59206.2023.10308501 - , , , , , :
Probabilistic prediction methods for nonlinear systems with application to stochastic model predictive control
In: Annual Reviews in Control 56 (2023), p. 100905
ISSN: 1367-5788
DOI: 10.1016/j.arcontrol.2023.100905 - , , :
Online learning and adaptation of nonlinear thermal networks for power inverters
49th Annual Conference of the IEEE Industrial Electronics Society (IECON 2023) (Marina Bay Sands (Singapore), 16. October 2023 - 19. October 2023) - , , :
Improved nonlinear estimation in thermal networks using machine learning
IEEE International Conference on Mechatronics (ICM 2023) (Loughborough (UK), 15. March 2023 - 17. March 2023)
In: Proc. IEEE International Conference on Mechatronics (ICM 2023, accepted) 2023
DOI: 10.1109/icm54990.2023.10102071 - , , , , :
Rack force estimation from standstill to high speeds by hybrid model design and blending
IEEE International Conference on Mechatronics (ICM 2023) (Loughborough (UK), 15. March 2023 - 17. March 2023)
DOI: 10.1109/ICM54990.2023.10102078 - , :
Performance prediction of NMPC algorithms with incomplete optimization
22nd IFAC World Congress (Yokohama, Japan, 9. July 2023 - 14. July 2023)
In: Proc. 22nd IFAC World Congress (accepted) 2023 - , , :
Robust meta-learning of vehicle yaw rate dynamics via conditional neural processes
62nd IEEE Conference on Decision and Control (CDC) (Marina Bay Sands (Singapore), 13. December 2023 - 15. December 2023)
In: Proc. 62nd IEEE Conference on Decision and Control (CDC) 2023
- , , , :
Nonlinear MPC of a Heavy-Duty Diesel Engine With Learning Gaussian Process Regression
In: IEEE Transactions on Control Systems Technology 30 (2022), p. 113-129
ISSN: 1063-6536
DOI: 10.1109/TCST.2021.3054650 - , , , :
Model predictive interaction control based on a path-following formulation
In: Proceedings IEEE International Conference on Mechatronics and Automation (ICMA) 2022
DOI: 10.1109/icma54519.2022.9856004 - , , , , :
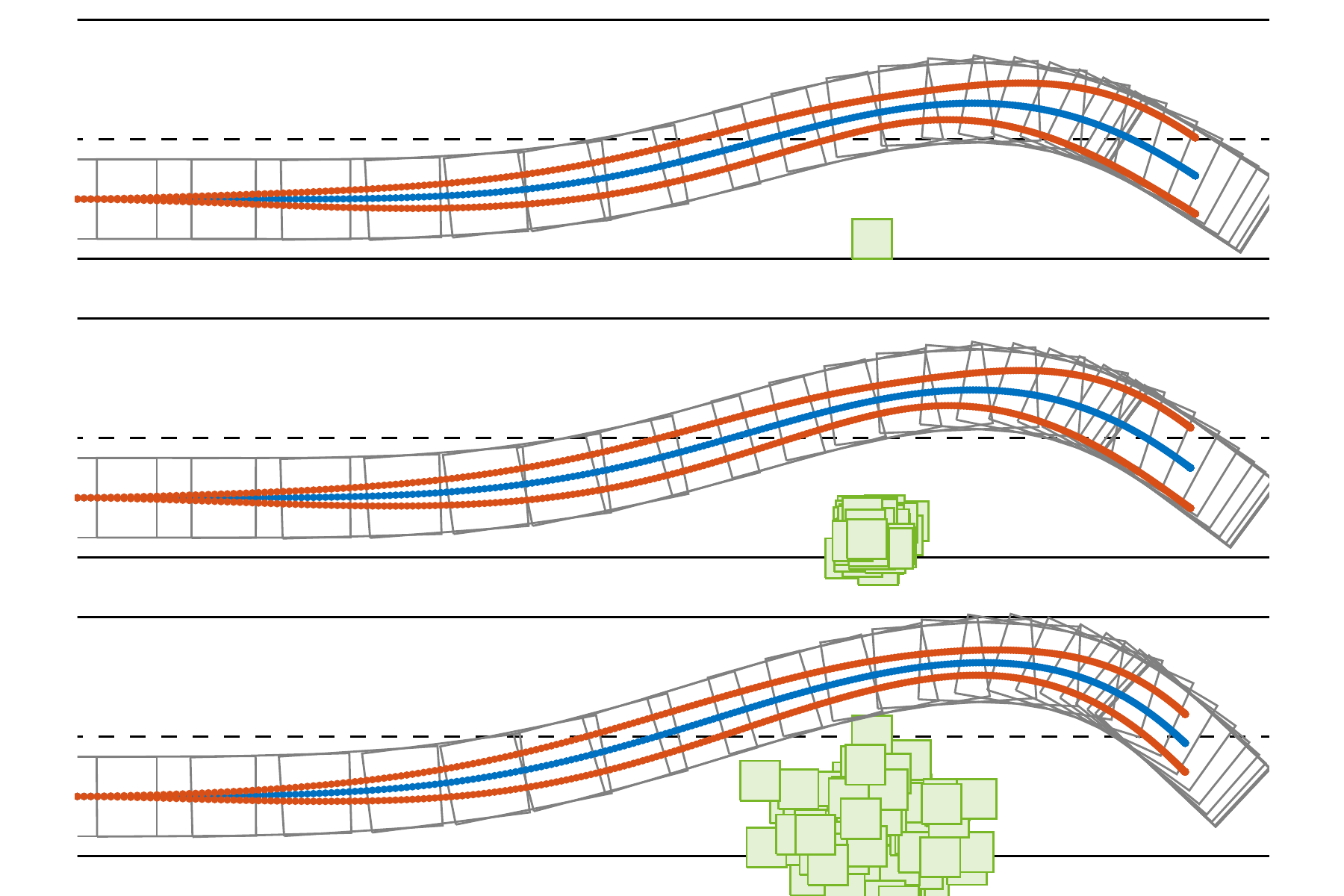
Hierarchical learning for model predictive collision avoidance
10th Vienna International Conference on Mathematical Modelling (MATHMOD 22) (Vienna (Austria), 27. July 2022 - 29. July 2022)
In: IFAC PapersOnLine 2022
DOI: 10.1016/j.ifacol.2022.09.121 - , , , :
Data-driven feed-forward control of hydraulic cylinders using Gaussian process regression for excavator assistance functions
6th IEEE Conference on Control Technology and Applications (CCTA) (Trieste (Italy), 22. August 2022 - 25. August 2022)
DOI: 10.1109/ccta49430.2022.9966062 - , , :
Dynamic and stationary state estimation of fluid cooled three-phase inverters
26th IEEE International Symposium on Power Electronics, Electrical Drives Automation and Motion (SPEEDAM 2022) (Sorrento (Italy), 22. June 2022 - 24. June 2022)
DOI: 10.1109/speedam53979.2022.9842247 - , , :
Semi-infinite programming using Gaussian process regression for robust design optimization
In: Proceedings European Control Conference 2022
DOI: 10.23919/ecc55457.2022.9838137
- , :
Safe Bayesian Optimization under Unknown Constraints
59th IEEE Conference on Decision and Control, CDC 2020 (, 14. December 2020 - 18. December 2020)
In: 59th IEEE Conference on Decision and Control (CDC 2020) 2020
DOI: 10.1109/CDC42340.2020.9304209 - , , , , :
Hierarchical Predictive Control of a Combined Engine/Selective Catalytic Reduction System with Limited Model Knowledge
In: SAE International Journal of Engines 13 (2020), p. 211-222
ISSN: 1946-3936
DOI: 10.4271/03-13-02-0015 - , , :
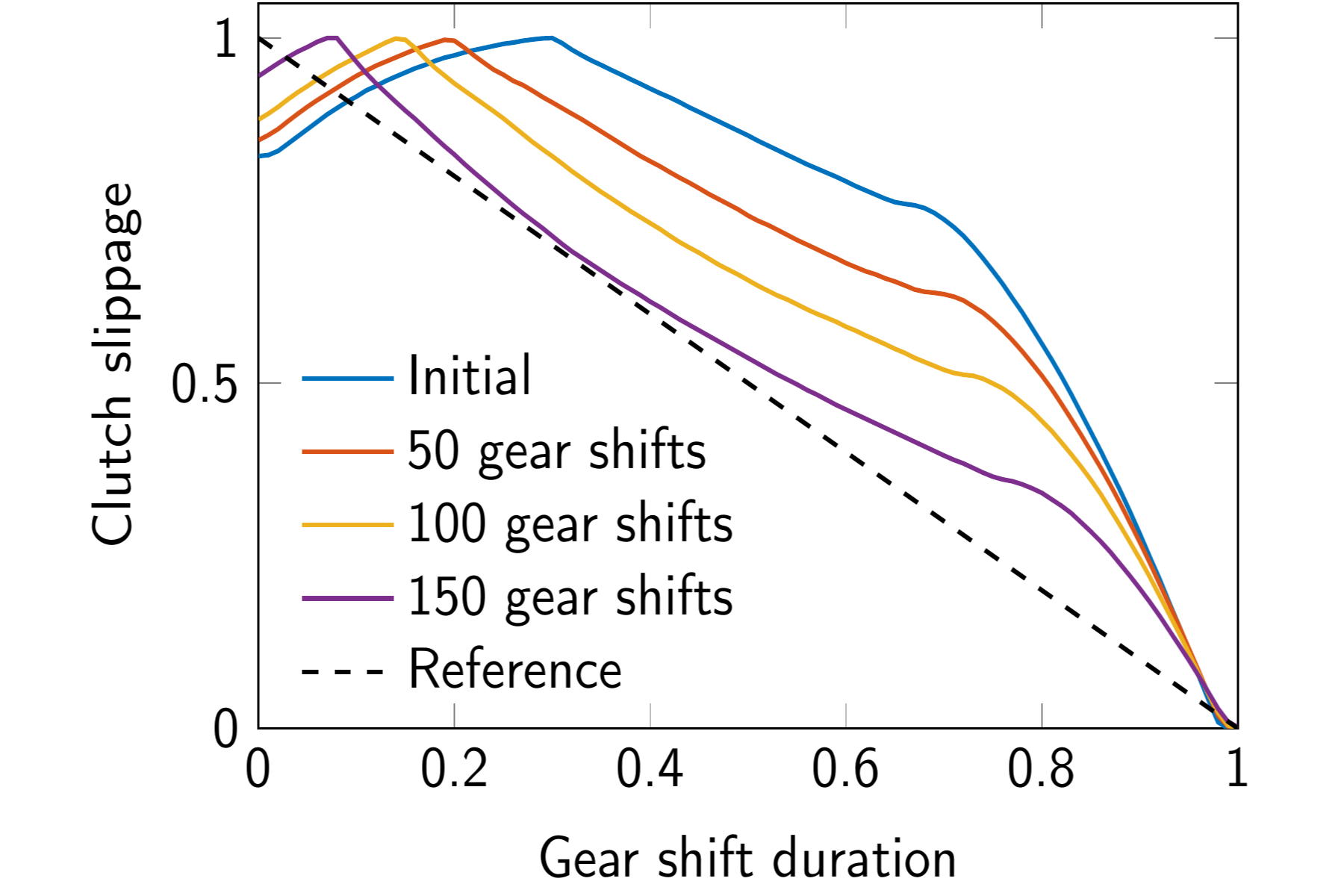
Learning feedforward control of a hydraulic clutch actuation path based on policy gradients
In: 59th IEEE Conference on Decision and Control (CDC 2020) 2020
DOI: 10.1109/cdc42340.2020.9303981