Learning in Control
Algorithms of artificial intelligence and machine learning are of increasing importance for control applications. Our research and expertise in this domain ranges from the modeling of unknown or uncertain dynamics over iterative and reinforcement learning to Bayesian optimization.
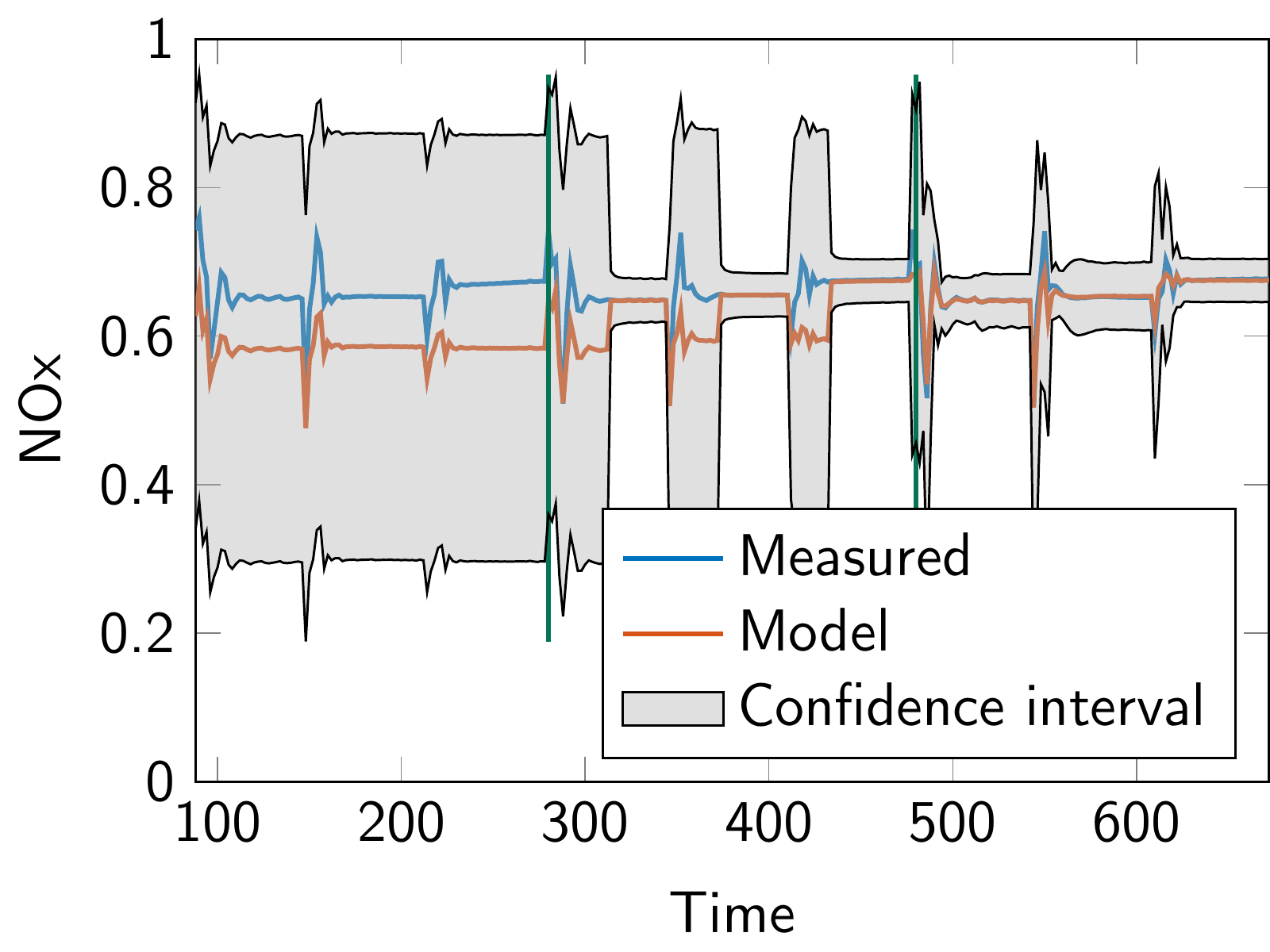
One research focus at the Chair is on learning in model design and identification. Hybrid and data-driven models are attractive if physical modeling is either poor or requires high effort. Practical applications often require an online adaptation of these models in order to reflect effects of aging or wear or to increase the model accuracy in different operation regimes. Information about the reliability and trustworthiness of a learned model can directly be used within the control design. For instance, the prediction of the uncertainty allows to satisfy constraints with a given probability. A challenge with learning-based methods is to ensure real-time feasibility with possibly weak hardware resources in order to bring these advanced learning in control methods into practice.
Another field of research and expertise is learning in optimization and control, for instance, reinforcement learning and Bayesian optimization. Reinforcement learning aims at obtaining an optimal control strategy from repeated interactions with the system. Formulating this task as an optimization problem shows the conceptual similarity to model predictive control, with the difference that reinforcement learning does not require model knowledge of the system. In a similar spirit, Bayesian optimization allows to solve complex optimization problem, in particular if the cost function or constraints are not analytically known or can only be evaluated by costly numerical simulations. Many technical tasks such as the optimization of production processes, an optimal product design or the search of optimal controller setpoints can be formulated as (partially) unknown optimization problem, illustrating the generality and importance of Bayesian optimization.
Related projects since 2021
AGENT-2: Predictive and learning control methods
To achieve climate targets, CO2 emissions in the building sector have to be significantly reduced. However, the integration of renewable energy sources increases the complexity of building energy systems and thus the requirements for the operation strategy. Model-based and predictive controllers are necessary for efficient operation. However, due to the high complexity of the energy systems, the development, implementation, and commissioning are very complex leading to high costs, which is why…
AUTOtech.agil: Robust Planning and Control using Probabilistic Methods
Anomaly detection and intelligent recalibration of sensorized systems
KI-unterstützte Modellierung zur Steigerung der Regelgüte
Kinesthetic teaching and predictive control of interaction tasks in robotics
Precise interactions as part of industrial manufacturing tasks are typically very complex to characterize and implement. One reason for this is the heterogeneity of the task-specific requirements for the motion and control behavior. A direct implementation of the task into a robot program therefore requires highly qualified specialists and is only profitable for large lot sizes. For a flexible applicability and easy (re-)configuration of the robot system, an approach to programming by kinesthetic…
Robust Reinforcement Learning for Thermal Management Control
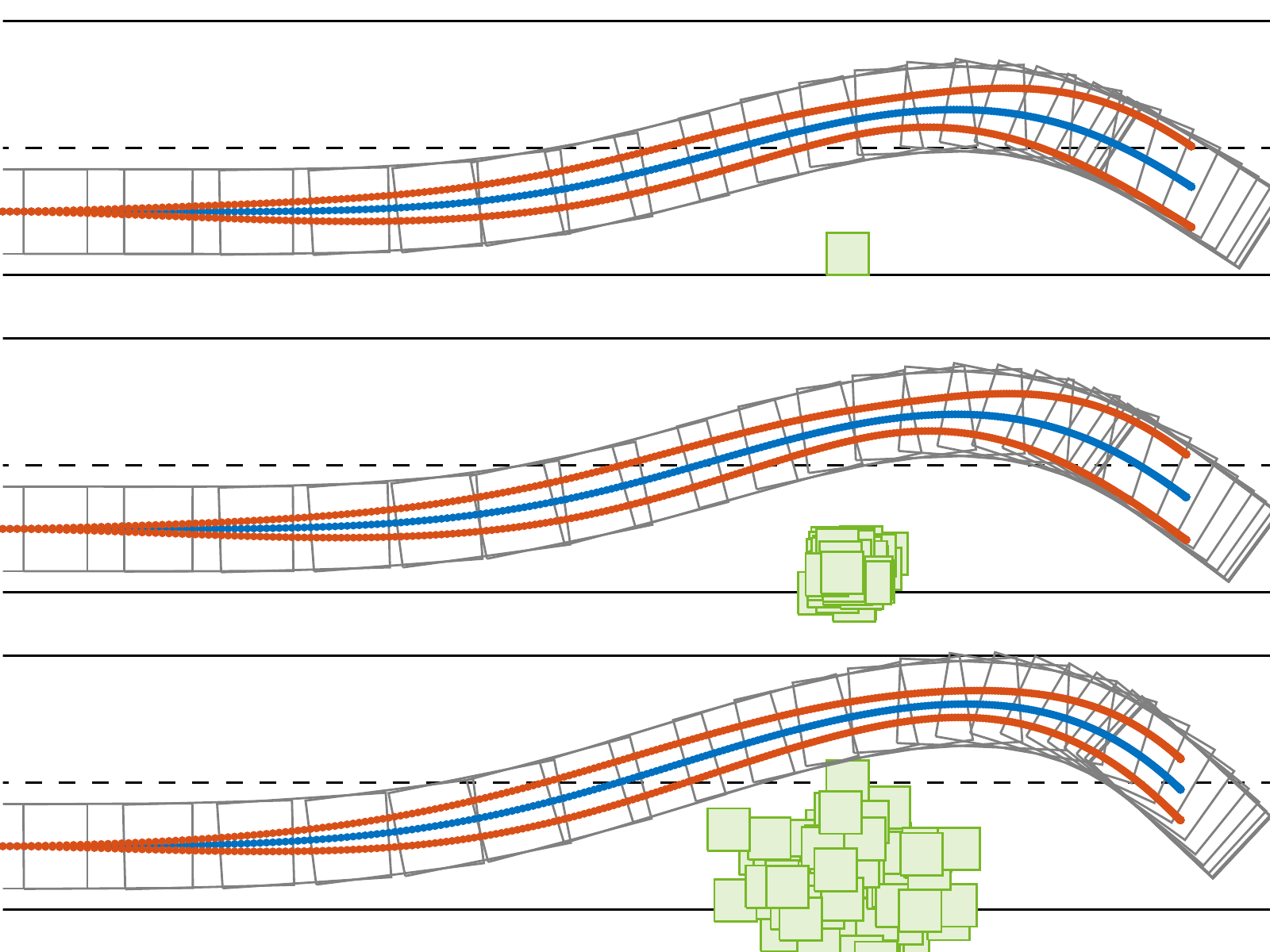
KARMA: Development of an innovative camera-based framework for collision-free human-machine movement
Related publications
Since 2021
- Bergmann, D., Harder, K., Niemeyer, J., & Graichen, K. (2022). Nonlinear MPC of a Heavy-Duty Diesel Engine With Learning Gaussian Process Regression. IEEE Transactions on Control Systems Technology, 30(1), 113-129. https://doi.org/10.1109/TCST.2021.3054650
- Stecher, J., Kiltz, L., & Graichen, K. (2022). Semi-infinite programming using Gaussian process regression for robust design optimization. In Proceedings European Control Conference (pp. 52-59). London (UK).
- Rabenstein, G., Demir, O., Trachte, A., & Graichen, K. (2022). Data-driven feed-forward control of hydraulic cylinders using Gaussian process regression for excavator assistance functions. In Proceedings of the 6th IEEE Conference on Control Technology and Applications (CCTA). Trieste (Italy).
- Landgraf, D., Völz, A., Kontes, G., Graichen, K., & Mutschler, C. (2022). Hierarchical learning for model predictive collision avoidance. In IFAC PapersOnLine (pp. 355-360). Vienna (Austria).
- Dio, M., Demir, O., Trachte, A., & Graichen, K. (2023). Safe active learning and probabilistic design of experiment for autonomous hydraulic excavators. In Proceedings of the 2023 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). Detroit, US.
- Bergmann, D., Harder, K., Niemeyer, J., & Graichen, K. (2022). Nonlinear MPC of a Heavy-Duty Diesel Engine With Learning Gaussian Process Regression. IEEE Transactions on Control Systems Technology, 30(1), 113-129. https://doi.org/10.1109/TCST.2021.3054650
- Stecher, J., Kiltz, L., & Graichen, K. (2022). Semi-infinite programming using Gaussian process regression for robust design optimization. In Proceedings European Control Conference (pp. 52-59). London (UK).
- Rabenstein, G., Demir, O., Trachte, A., & Graichen, K. (2022). Data-driven feed-forward control of hydraulic cylinders using Gaussian process regression for excavator assistance functions. In Proceedings of the 6th IEEE Conference on Control Technology and Applications (CCTA). Trieste (Italy).
- Landgraf, D., Völz, A., Kontes, G., Graichen, K., & Mutschler, C. (2022). Hierarchical learning for model predictive collision avoidance. In IFAC PapersOnLine (pp. 355-360). Vienna (Austria).
- Dio, M., Demir, O., Trachte, A., & Graichen, K. (2023). Safe active learning and probabilistic design of experiment for autonomous hydraulic excavators. In Proceedings of the 2023 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). Detroit, US.
2020
- Bergmann, D., & Graichen, K. (2020). Safe Bayesian Optimization under Unknown Constraints. In 59th IEEE Conference on Decision and Control (CDC 2020) (pp. 3592-3597). Institute of Electrical and Electronics Engineers Inc..
- Geiselhart, R., Bergmann, D., Niemeyer, J., Remele, J., & Graichen, K. (2020). Hierarchical Predictive Control of a Combined Engine/Selective Catalytic Reduction System with Limited Model Knowledge. SAE International Journal of Engines, 13(2). https://doi.org/10.4271/03-13-02-0015
- Geiselhart, R., Bergmann, D., Niemeyer, J., Remele, J., & Graichen, K. (2020). Hierarchical predictive control of a combined engine/SCR system with limited model knowledge. SAE International Journal of Engines, 13(2). https://doi.org/10.4271/03-13-02-0015
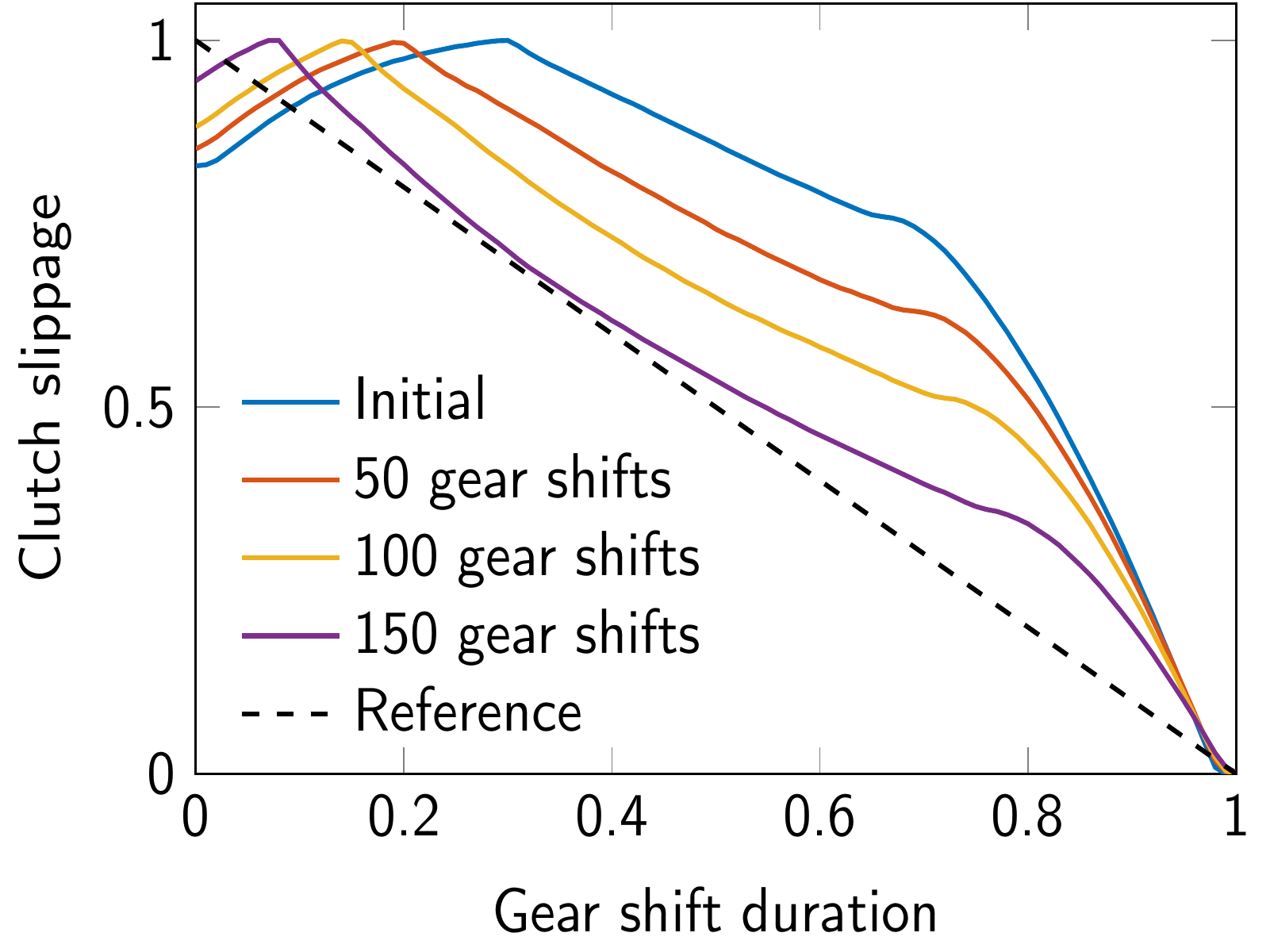
- Mesmer, F., Szabo, T., & Graichen, K. (2020). Learning feedforward control of a hydraulic clutch actuation path based on policy gradients. In 59th IEEE Conference on Decision and Control (CDC 2020).
- Bergmann, D., & Graichen, K. (2020). Safe Bayesian Optimization under Unknown Constraints. In 59th IEEE Conference on Decision and Control (CDC 2020) (pp. 3592-3597). Institute of Electrical and Electronics Engineers Inc..
- Geiselhart, R., Bergmann, D., Niemeyer, J., Remele, J., & Graichen, K. (2020). Hierarchical Predictive Control of a Combined Engine/Selective Catalytic Reduction System with Limited Model Knowledge. SAE International Journal of Engines, 13(2). https://doi.org/10.4271/03-13-02-0015
- Geiselhart, R., Bergmann, D., Niemeyer, J., Remele, J., & Graichen, K. (2020). Hierarchical predictive control of a combined engine/SCR system with limited model knowledge. SAE International Journal of Engines, 13(2). https://doi.org/10.4271/03-13-02-0015
- Mesmer, F., Szabo, T., & Graichen, K. (2020). Learning feedforward control of a hydraulic clutch actuation path based on policy gradients. In 59th IEEE Conference on Decision and Control (CDC 2020).
2019 and earlier
- Mesmer, F., Szabo, T., & Graichen, K. (2019). Learning methods for the feedforward control of a hydraulic clutch actuation path. In Proc. IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM 2019) (pp. 733-738). Hong Kong (China).
- Bergmann, D., Geiselhart, R., & Graichen, K. (2019). Modelling and control of a heavy-duty Diesel engine gas path with Gaussian process regression. In Proc. European Control Conference (ECC 2019) (pp. 1207-1213). Naples (Italy).
- Bergmann, D., & Graichen, K. (2019). Gaußprozessregression zur Modellierung zeitvarianter Systeme. At-Automatisierungstechnik, 67(8), 637-647. https://doi.org/10.1515/auto-2019-0015
- Mesmer, F., Szabo, T., & Graichen, K. (2019). Learning methods for the feedforward control of a hydraulic clutch actuation path. In Proc. IEEE/ASME International Conference on Advanced Intelligent Mechatronics (AIM 2019) (pp. 733-738). Hong Kong (China).
- Bergmann, D., Geiselhart, R., & Graichen, K. (2019). Modelling and control of a heavy-duty Diesel engine gas path with Gaussian process regression. In Proc. European Control Conference (ECC 2019) (pp. 1207-1213). Naples (Italy).
- Bergmann, D., & Graichen, K. (2019). Gaußprozessregression zur Modellierung zeitvarianter Systeme. At-Automatisierungstechnik, 67(8), 637-647. https://doi.org/10.1515/auto-2019-0015