Control & Optimization
The development of control and optimization methods for dynamical systems is the natural research focus of the Chair of Automatic Control. In particular, we focus on nonlinear and predictive control concepts as well as path/trajectory planning for dynamical systems closely related to optimization-based methods, always having an eye on the real-time and embedded realization for practical applications.
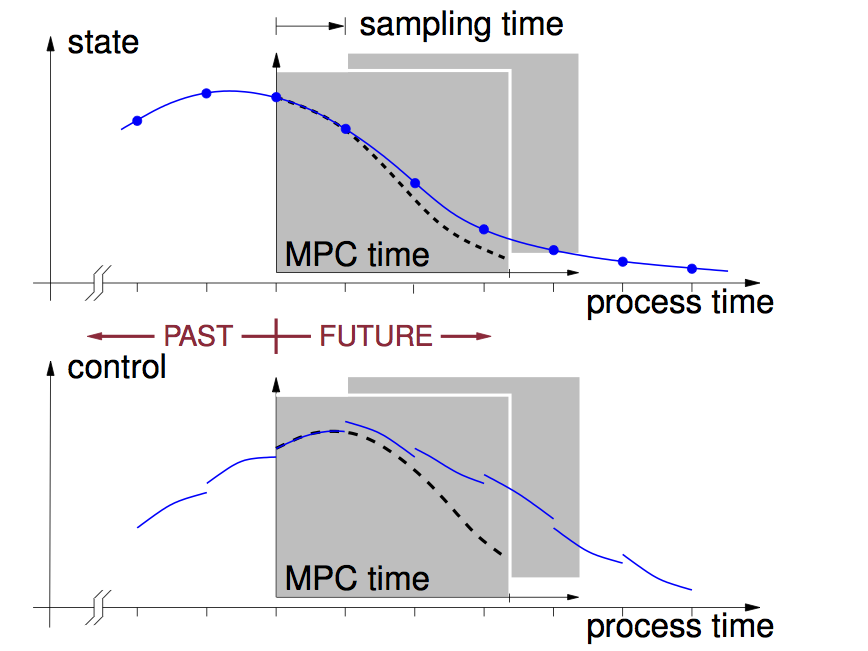
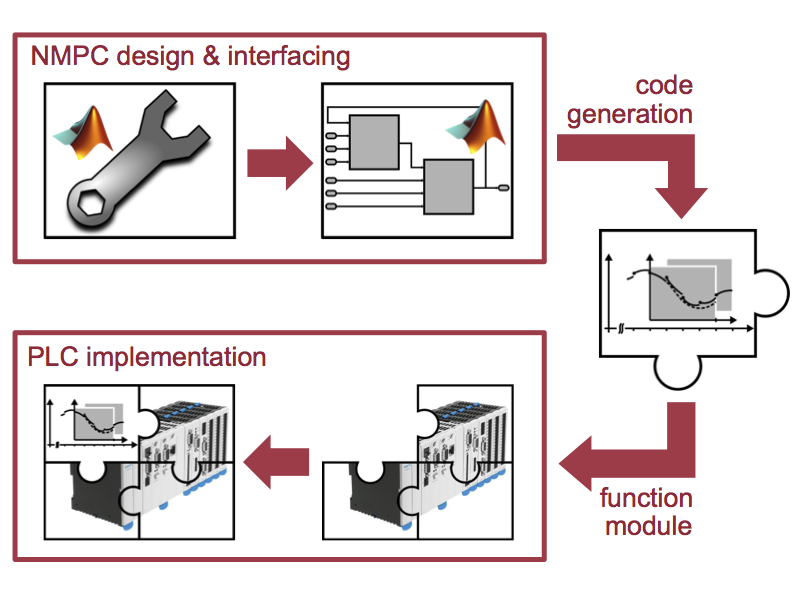
Research on nonlinear systems and control is at the heart of the Chair of Automatic Control. Modern control concepts such as model predictive control (MPC) often rely on optimization problems that have to be solved online. In particular mechatronic systems often require sampling times in the (sub-)millisecond range and therefore highly efficient control algorithms and warm-start strategies. The Chair of Automatic Control has long standing experience with the modeling of control problems of different physical domains and the development of nonlinear and predictive control concepts, always with the intention to bring these methods into practice. We also develop and maintain the open source MPC toolbox GRAMPC that was successfully used in many research and industrial projects and by other research groups. Current research concerns the extension to stochastic nonlinear systems to account for uncertainties in a consistent probabilistic setting.
Beyond the “classical” centralized view on control applications, networked systems are of increasing importance, not only in terms of autonomous and mobile robots, distributed energy networks (smart grids), but also in connection with industry 4.0 and flexible production. The control of networked systems is challenging, because centralized approaches do not scale well with the number of subsystems and do not provide the flexibility for plug-and-play or reconfiguration scenarios. We focus on both the design of distributed (model predictive) control schemes for networked systems as well as the agent-based distributed implementation of these concepts along with suitable communication concepts to enhance the overall efficiency of networked systems. An outcome of this research is the open-source framework GRAMPC-D that implements a real-time efficient ADMM algorithm for distributed model predictive control of nonlinear networked systems including plug-and-play functionality.
Videos
Related projects since 2021
Term: 1. November 2021 - 31. October 2024
Funding source: Industrie
Project leader:
Funding source: Industrie
Project leader:
Term: 1. July 2021 - 30. June 2024
Funding source: Bayerische Forschungsstiftung
Project leader:
Funding source: Bayerische Forschungsstiftung
Project leader:
Term: 1. February 2022 - 31. January 2025
Funding source: Industrie
Project leader:
Funding source: Industrie
Project leader:
Term: 1. September 2022 - 31. August 2025
Funding source: DFG-Einzelförderung / Sachbeihilfe (EIN-SBH)
Project leader:
Funding source: DFG-Einzelförderung / Sachbeihilfe (EIN-SBH)
Project leader:
Dual-armrobots offer a high potential for automation technology, as they canbe used to implement tasks that are not possible with one arm alone.This includes in particular the manipulation of large or heavyobjects that exceed the payload of a single arm. Illustrativeexamples are the movement of beverage crates, long boards or pipes,which are also preferably grasped by humans with both hands.
However,cooperative manipulation is particularly challenging, because botharms…
Term: 1. January 2022 - 31. December 2024
Funding source: Deutsche Forschungsgemeinschaft (DFG)
Project leader:
Funding source: Deutsche Forschungsgemeinschaft (DFG)
Project leader:
Term: 1. January 2023 - 31. December 2025
Funding source: DFG / Schwerpunktprogramm (SPP)
Project leader: , ,
Funding source: DFG / Schwerpunktprogramm (SPP)
Project leader: , ,
The aim of this project is the automated production of liquid-liquid disperse systems via melt emulsification, whereby in this process emulsification takes place at elevated temperature. The products obtained after cooling are dispersions of spherical nanoparticles or microparticles. Within the scope of this project, a melt emulsification device for the automated production of product particles with a well-defined particle size distribution (PSD) will be further developed. The PSD has a significant influence on the subsequent product properties, such as flow behavior or drug release kinetics. The PSD of the products is determined by the complex interaction of competing mechanisms. These are, in particular, droplet breakup in a rotor-stator device as a result of shear and elongation stress, as well as coalescence and further ripening, which in turn depend on the system composition, i.e. the emulsifier used (type, concentration) and the dispersion phase (viscosity, volume fraction).
Therefore, for a better process understanding and an active process control, possibilities for in situ determination of the PSD are urgently required. In this project, a novel fiber-coupled measurement system based on broadband elastic light scattering is developed for in situ measurement of the PSD. The system will be validated on reference particle systems and applied to the emulsification process. Furthermore, a hybrid process model is developed, which is the basis for the design of a model predictive control of the process. The model predictive control in combination with the in situ measurement will provide the possibility for an active process control and the production of emulsions with predefined properties and a simultaneous optimization of the process time.
Related publications
- Hartmann P, Graichen K (2025). Learning-based uncertainty-aware predictive control of truck-trailer systems in rough terrain. In 19th IEEE International Conference on Control & Automation (ICCA) (accepted).
- Kruse T, Griebel T, Graichen K (2025). Adaptive Kalman filtering: Measurement and process noise covariance estimation using Kalman smoothing. IEEE Access, 13, 11863-11875. [DOI].
- Landgraf D, Wietzke T, Graichen K (2025). Stochastic model predictive control with switched latent force models. In European Control Conference.
- Pierer von Esch M, Nistler E, Völz A, Graichen K (2025). Sensitivity-based distributed NMPC: Experimental results for a levitating planar motion system. IEEE Transactions on Control Systems Technology. [DOI].
- Pierer von Esch M, Völz A, Graichen K (2025). A fixed-point iteration scheme for sensitivity-based distributed optimal control. IEEE Transactions on Automatic Control, 70(4), 2778-2785. [DOI].
- Pierer von Esch M, Völz A, Graichen K (2025). Asynchronous sensitivity-based distributed optimal control for nonlinear systems. In 2025 American Control Conference (ACC).
- Pierer von Esch M, Völz A, Graichen K (2025). Sensitivity-Based Distributed Model Predictive Control for Nonlinear Systems under Inexact Optimization. Optimal Control Applications & Methods, (accepted).
- Cherian AJ, Michalka A, Murray K, Roell G, Graichen K (2024). Control approaches for operating point stabilization of microring resonator modulators under fast perturbations. In Silicon Photonics XIX (pp. 128910D). [DOI].
- Conrad P, Graichen K (2024). A sensitivity-based approach to self-triggered nonlinear model predictive control. IEEE Access, 12, 153243-153252. [DOI].
- Dahlmann J, Graichen K, Völz A (2024). Ein Konzept zum automatisierten Rangieren von Fahrzeugen mit Anhängern. At-Automatisierungstechnik, 72(4), 354-368. [DOI].
- Dahlmann J, Völz A, Lukassek M, Graichen K (2024). Local predictive optimization of globally planned motions for truck-trailer systems. IEEE Transactions on Control Systems Technology, 32(5), 1555-1568. [DOI].
- Goppelt-Schneider F, Schmidt-Vollus R, Graichen K (2024). Trajectory tracking control for multilevel pressure boosting systems. In 28th International Conference on System Theory, Control and Computing (ICSTCC).
- Kißkalt J, Michalka A, Strohmeyer C, Horn M, Graichen K (2024). Fault detection in gauge-sensorized strain wave gears. In European Control Conference (pp. 26-33). [DOI].
- Lukassek M, Dahlmann J, Völz A, Graichen K (2024). Model predictive path-following control for truck–trailer systems with specific guidance points – Design and experimental validation. Mechatronics, 100, 103190. [DOI].
- Löhe K, Reinhard J, Petrasch N, Kallabis S, Graichen K, Mucha M (2024). Work Roll Speed Drop Compensation for Hot Strip Mills Reduces Drivetrain Wear and Increases Strip Quality. In AISTech 2024 Iron and Steel Technology Conference (pp. 1212-1223). Warrendale, PA. [DOI].
- Pierer von Esch M, Landgraf D, Steffel M, Völz A, Graichen K (2024). Distributed stochastic optimal control of nonlinear systems based on ADMM. In 63th IEEE Conference on Decision and Control (CDC 2024).
- Pierer von Esch M, Landgraf D, Steffel M, Völz A, Graichen K (2024). Distributed Stochastic Optimal Control of Nonlinear Systems based on ADMM. IEEE Control Systems Letters, 8, 424-429. [DOI].
- Pierer von Esch M, Völz A, Graichen K (2024). Sensitivity-Based Distributed Model Predictive Control: Synchronous and Asynchronous Execution Compared to ADMM. At-Automatisierungstechnik, 72(2), 91-106. [DOI].
- Pierer von Esch M, Völz A, Graichen K (2024). Asynchronous ADMM for Nonlinear Continuous-Time Systems. Optimal Control Applications & Methods.
- Pierer von Esch M, Völz A, Graichen K (2024). Sensitivity-based distributed model predictive control: synchronous and asynchronous execution compared to ADMM. At-Automatisierungstechnik, 72(2), 91-106. [DOI].
- Reinhard J, Löhe K, Graichen K (2024). Optimal dynamic current control for externally excited synchronous machines. In 2024 IEEE Conference on Control Technology and Applications (CCTA) (pp. 146-152). [DOI].
- Reinhard J, Löhe K, Petrasch N, Kallabis S, Graichen K (2024). Dynamic compensation of the threading speed drop in rolling processes. Journal of Process Control, 137, 103197. [DOI].
- Südhoff T, Ebner L, Schmidt J, Graichen K (2024). GP-based modeling for PSD control of emulsification processes. In 28th International Conference on System Theory, Control and Computing (ICSTCC).
- Dio M, Völz A, Graichen K (2023). Cooperative dual-arm control for heavy object manipulation based on hierarchical quadratic programming. In 2023 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) (pp. 643-648).
- Gold T, Völz A, Graichen K (2023). Model predictive interaction control for robotic manipulation tasks. IEEE Transactions on Robotics, 39(1), 76-89. [DOI].
- Harder K, Niemeyer J, Remele J, Graichen K (2023). Hierarchical model predictive control for an off-highway Diesel engine with SCR catalyst. International Journal of Engine Research. [DOI].
- Kißkalt J, Michalka A, Strohmeyer C, Horn M, Graichen K (2023). Simulation chain for sensorized strain wave gears. In 27th International Conference on System Theory, Control and Computing (ICSTCC) (pp. 467 – 473). [DOI].
- Landgraf D, Völz A, Berkel F, Schmidt K, Specker T, Graichen K (2023). Probabilistic prediction methods for nonlinear systems with application to stochastic model predictive control. Annual Reviews in Control, 56, 100905. [DOI].
- Spenger P, Graichen K (2023). Performance prediction of NMPC algorithms with incomplete optimization. In 22nd IFAC World Congress (pp. 7456-7461).
- Burk D, Völz A, Graichen K (2022). A modular framework for distributed model predictive control of nonlinear continuous-time systems (GRAMPC-D). Optimization and Engineering, 23, 771-795. [DOI].
- Burk D, Völz A, Graichen K (2022). Improving the performance of distributed model predictive control by applying graph partitioning methods. In 26th International Conference on System Theory, Control and Computing (ICSTCC). [DOI].
- Dahlmann J, Volz A, Szabo T, Graichen K (2022). A Numerical Approach for Solving the Inversion Problem for n-Trailer Systems. In 2022 American Control Conference, ACC 2022 (pp. 2018-2024). Proceedings of the American Control Conference, 2022-June, 2018-2024. [DOI].
- Dahlmann J, Völz A, Szabo T, Graichen K (2022). A numerical approach for solving the inversion problem for general n-trailer systems.. In Proceedings 2022 American Control Conference (ACC) (pp. 2018-2024). [DOI].
- Dahlmann J, Völz A, Szabo T, Graichen K (2022). Trajectory optimization for truck-trailer systems based on predictive path-following control. In 6th IEEE Conference on Control Technology and Applications (CCTA). [DOI].
- Gold T, Römer R, Völz A, Graichen K (2022). Catching objects with a robot arm using model predictive control. In Proceedings 2022 American Control Conference (ACC) (pp. 1915-1920). [DOI].
- Huber H, Burk D, Graichen K (2022). Comparison of sensitivity-based and ADMM-based DMPC applied to building automation. In 6th IEEE Conference on Control Technology and Applications (CCTA) (pp. 546-553). [DOI].
- Kowalewski J, Lorenz A, Lomakin A, Alvarez R, Graichen K (2022). Circulating current control and energy balancing of a modular multilevel converter using model predictive control for HVDC applications. In 48th Annual Conference of the IEEE Industrial Electronics Society (IECON 2022). [DOI].
- Lamprecht A, Steffen D, Nagel K, Häcker J, Graichen K (2022). Online Model Predictive Motion Cueing With Real-Time Driver Prediction. IEEE Transactions on Intelligent Transportation Systems, 23(8), 12414-12428. [DOI].
- Landgraf D, Völz A, Graichen K (2022). Nonlinear model predictive control with latent force models. In Proceedings 2022 American Control Conference (ACC) (pp. 4979-4984). [DOI].
- Landgraf D, Völz A, Kontes G, Graichen K, Mutschler C (2022). Hierarchical learning for model predictive collision avoidance. In 10th Vienna International Conference on Mathematical Modelling (MATHMOD 22) (pp. 355-360). [DOI].
- Reinhard J, Löhe K, Graichen K (2022). Optimal current setpoint computation for externally excited synchronous machines. In 6th IEEE Conference on Control Technology and Applications (CCTA) (pp. 1319-1326). [DOI].
- Snobar F, Reinhard J, Huber H, Hoffmann M, Stelzig M, Vossiek M, Graichen K (2022). FOV-based model predictive object tracking for quadcopters. In 9th IFAC Symposium on Mechatronic Systems (Mechatronics 2022) (pp. 13 – 18). [DOI].
- Stecher J, Kiltz L, Graichen K (2022). Semi-infinite programming using Gaussian process regression for robust design optimization. In Proceedings European Control Conference (pp. 52-59). [DOI].
- Burk D, Völz A, Graichen K (2021). Experimental validation of the open-source DMPC framework GRAMPC-D applied to the remote-accessible robotarium. In IEEE International Conference on Mechatronics and Automation (ICMA). [DOI].
- Burk D, Völz A, Graichen K (2021). Towards asynchronous ADMM for distributed model predictive control of nonlinear systems. In Proceedings European Control Conference (ECC 2021) (pp. 1950-1955). [DOI].
- Gold T, Rohrmüller M, Völz A, Graichen K (2021). Model predictive interaction control for force closure grasping. In 2021 IEEE Conference on Decision and Control (CDC) (pp. 1018-1023). [DOI].
- Huber H, Graichen K (2021). A sensitivity-based distributed model predictive control algorithm for nonlinear continuous-time systems. In 5th IEEE Conference on Control Technology and Applications (CCTA) (pp. (accepted)). [DOI].
- Lamprecht A, Emmert T, Graichen K (2021). Learning-based driver prediction for MPC-based motion cueing algorithms. In Driving Simulation Conference Europe 2021 (DSC) (pp. 133 – 140).
- Lamprecht A, Steffen D, Häcker J, Graichen K (2021). Potential der modellprädiktiven Regelung für Fahrsimulatoren. At-Automatisierungstechnik, 69(2), 155-170. [DOI].
- Lukassek M, Völz A, Szabo T, Graichen K (2021). Model predictive path-following control for general n-trailer systems with an arbitrary guidance point. In Proceedings European Control Conference (ECC 2021) (pp. 1329-1334). [DOI].
- Völz A, Graichen K (2021). Gradient-based nonlinear model predictive control for systems with state-dependent mass matrix. In 2021 IEEE Conference on Decision and Control (CDC), accepted. [DOI].
- Burk D, Völz A, Graichen K (2020). Distributed optimization with ALADIN for non-convex optimal control problems. In 59th IEEE Conference on Decision and Control (CDC 2020). [DOI].
- Burk D, Völz A, Graichen K (2020). Neighbor approximations for distributed optimal control of nonlinear networked systems. In European Control Conference (ECC 2020) (pp. 1238-1243). [DOI].
- Englert T, Graichen K (2020). Nonlinear model predictive torque control and setpoint computation of induction machines for high performance applications. Control Engineering Practice, 99. [DOI].
- Gold T, Lomakin A, Goller T, Völz A, Graichen K (2020). Towards a Generic Manipulation Framework for Robots based on Model Predictive Interaction Control. In IEEE International Conference on Mechatronics and Automation (ICMA) (pp. 401 – 407). [DOI].
- Gold T, Völz A, Graichen K (2020). Model Predictive Interaction Control for Industrial Robots. In 21st IFAC World Congress (pp. 10026 – 10033). [DOI].
- Gold T, Völz A, Graichen K (2020). Model Predictive Position and Force Trajectory Tracking Control for Robot-Environment Interaction. In 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS) (pp. 7397-7402). [DOI].
- Kruse T, Graichen K (2020). Moving horizon estimation for continuous glucose monitoring. In 7th International Conference on Biomedical Engineering and Systems (ICBES 20). [DOI].
- Lomakin A, Mayr A, Graichen K, Franke J (2020). Optimization of direct winding processes based on a holistic control approach. In Electric Drives Production Conference (E-DPC). [DOI].
- Lukassek M, Völz A, Szabo T, Graichen K (2020). Model predictive control for agricultural machines with implements. In Proceedings 28th Mediterranean Conference on Control and Automation (MED) (pp. 387-392). [DOI].
- Bestler A, Graichen K (2019). Distributed model predictive control for continuous-time nonlinear systems based on suboptimal ADMM. Optimal Control Applications & Methods, 40(1), 1-23. [DOI].
- Burk D, Völz A, Graichen K (2019). Towards a modular framework for distributed model predictive control of nonlinear neighbor-affine systems. In 58th IEEE Conference on Decision and Control (CDC 2019) (pp. 5279-5284). [DOI].
- Englert T, Völz A, Mesmer F, Rhein S, Graichen K (2019). A software framework for embedded nonlinear model predictive control using a gradient-based augmented Lagrangian approach (GRAMPC). Optimization and Engineering, 20(3), 769-809. [DOI].
- Gold T, Völz A, Graichen K (2019). External torque estimation for an industrial robot arm using joint torsion and motor current measurements. In Joint Conference 8th IFAC Symposium on Mechatronic Systems (MECHATRONICS) and 11th IFAC Symposium on Nonlinear Control Systems (NOLCOS) (pp. 879-884). Vienna (Austria). [DOI].
- Lamprecht A, Steffen D, Häcker J, Graichen K (2019). Comparison between a Filter- and an MPC-based MCA in an Offline Simulator Study. In Driving Simulation Conference & Exhibition (DSC) (pp. 101-107).
- Lamprecht A, Steffen D, Häcker J, Graichen K (2019). Optimal control based reference generation for model predictive motion cueing algorithms. In 3rd IEEE Conference on Control Technology and Application (CCTA 2019) (pp. 203-208). Hong Kong (China). [DOI].
- Englert T, Graichen K (2018). A fixed-point iteration scheme for model predictive torque control of PMSMs. In Proceedings 6th IFAC Conference on Nonlinear Model Predictive Control (NMPC) (pp. 668-673). Madison, WI (USA).
- Harder K, Buchholz M, Späder T, Graichen K (2018). A real-time nonlinear air path observer for off-highway diesel engines. In Proceedings 2018 European Control Conference (ECC) (pp. 237-242). Limassol (Cyprus).
- Lamprecht A, Häcker J, Graichen K (2018). Constrained motion cueing for driving simulators using a real-time nonlinear MPC scheme. In Proceedings 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (pp. 7466-7471). Madrid (Spain).
- Rhein S, Graichen K (2018). Constrained trajectory planning and actuator design for electromagnetic heating systems. Control Engineering Practice, 74, 191-203.
- Graichen K, Hentzelt S (2015). A bi-level nonlinear predictive control scheme for hopping robots with hip and tail actuation. In Proceedings 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2015) (pp. 4480-4485). Hamburg (Germany).
- Hentzelt S, Graichen K (2014). Experimental results for distributed model predictive control applied to a water distribution system. In Proceedings 2014 IEEE Multi-Conference on Systems and Control (pp. 1100-1106). Nice (France).
- Kaepernick B, Graichen K (2014). PLC implementation of a nonlinear model predictive controller. In Proceedings 19th IFAC World Congress (pp. 1892-1897). Cape Town (South Africa).
- Käpernick B, Graichen K (2014). Nichtlineare modellprädiktive Regelung auf SPS. Automatisierungstechnische Praxis, 56, 38-46. [DOI].
- Käpernick B, Graichen K (2014). The gradient based nonlinear model predictive control software GRAMPC. In Proceedings 13th European Control Conference (ECC) (pp. 1170-1175). Strasbourg (France).
- Käpernick B, Süß S, Schubert E, Graichen K (2014). A synthesis strategy for nonlinear model predictive controller on FPGA. In Proceedings 2014 UKACC 10th International Conference on Control (pp. 662-667). Loughborough (UK).
- Rhein S, Utz T, Graichen K (2014). Efficient state constraint handling for MPC of the heat equation. In Proceedings 2014 UKACC 10th International Conference on Control (pp. 663-668). Loughborough (UK).
- Utz T, Rhein S, Graichen K (2014). Transformation approach to constraint handling in optimal control of the heat equation. In Proceedings 19th IFAC World Congress (pp. 9135-9140). Cape Town (South Africa).
- Hentzelt S, Graichen K (2013). An augmented Lagrangian method in distributed dynamic optimization based on approximate neighbor dynamics. In Proceedings IEEE Intern. Conf. Systems, Man, and Cybernetics (SMC 2013) (pp. 571-576). Manchester (UK).
- Käpernick B, Graichen K (2013). Transformation of output constraints in optimal control applied to a double pendulum on a cart. In Proceedings 9th IFAC Symposium “Nonlinear Control Systems” (NOLCOS) (pp. 193-198). Toulouse (Italy).
- Käpernick B, Graichen K (2013). Model predictive control of an overhead crane using constraint substitution. In Proceedings 2013 American Control Conference (ACC) (pp. 3979-3984). Washington, DC (USA).
- Käpernick B, Hentzelt S, Graichen K (2013). A parallelizable decomposition approach for constrained optimal control problems. In Proceedings 52th IEEE Conference on Decision and Control (CDC) (pp. 5783-5788). Florence (Italy).
- Rhein S, Utz T, Graichen K (2013). Model predictive control and moving horizon estimation of a large-scale chemical reactor model. In Proceedings 1st {IFAC} Symposium on Control of Systems Governed by Partial Differential Equations (CPDE) (pp. 121-126). Paris (France).
- Graichen K, Käpernick B (2012). A real-time gradient method for nonlinear model predictive control. In Zheng T (Eds.), Frontiers of Model Predictive Control, pp. 9-28. [DOI].
- Graichen K, Käpernick B (2012). Nonlinear MPC with systematic handling of a class of constraints. In Oberwolfach Report No. 12/2012 (Workshop “Control Theory: Mathematical Perspectives on Complex Networked Systems”) (pp. 17-18). Oberwolfach (Germany). [DOI].
- Hentzelt S, Graichen K (2012). Dual decomposition of optimal control problems with coupled nonlinear dynamics. In CD-ROM Proceedings European Congress on Computational Methods in Applied Sciences and Engineering (ECCOMAS 2012). Vienna (Austria).